Hydro and MHD Methods¶
There are four available methods in Enzo for calculating the evolution of the gas with and without magnetic fields. Below is a brief description of each method, including the parameters associated with each one and a link to further reading.
Method 0: Piecewise Parabolic Method (PPM)¶
Source: Grid_SolvePPM_DE.C
The PPM scheme uses a parabolic function to estimate the left and states of the Godunov problem. This more accurately represents both smooth gradients and discontinuities over linear interpolation, i.e. PLM.
Parameters¶
Main call: HydroMethod = 0
RiemannSolver: specifies the type of solver, where the following only works with the PPM solver.
- HLL (Harten-Lax-van Leer) a two-wave, three-state solver with no resolution of contact waves. This is the most diffusive of the available three solvers in PPM. New for version 2.1
- HLLC (Harten-Lax-van Leer with Contact) a three-wave, four-state solver with better resolution of contacts. The most resilient to rarefaction waves (e.g. blastwave interiors). New for version 2.1
- Default Two-shock approximation. Iterative solver.
RiemannSolverFallback: allows for the Riemann solver to “fallback” to the more diffusive HLL solver when negative energies or densities are computed. Only applicable when using the HLLC and Two-shock solvers. The fluxes in the failing cell are recomputed and used in the Euler update of the gas quantities. New for version 2.1
ConservativeReconstruction: When interpolating (PPM) to the left and right states, interpolation occurs in the conserved variables (density, momentum, and energy) instead of the primitive variables (density, velocity, and pressure). This results in more accurate results in unigrid simulations but can cause errors with AMR. See Section 4.2.2 (steps 1-5) and Appendices A1 and B1 in Stone et al. (2008, ApJS 178, 137). New for version 2.1
DualEnergyFormalism: allows the total and thermal energy to be followed seperately during the simulation. Helpful when the velocities are high such that Etotal>> Ethermal.
PPMFlatteningParameter
PPMSteepeningParameter
Method 2: ZEUS¶
Source: ZeusSource.C, Zeus_xTransport.C, Zeus_yTransport.C, Zeus_zTransport.C, Grid_ZeusSolver.C, ZeusUtilities.C
ZEUS is a finite-difference method of solving hyperbolic PDEs instead of solving the Godunov problem. It is a very robust but relatively diffusive scheme.
Parameters¶
Main call: HydroMethod = 2
ZEUSQuadraticArtificialViscosity
ZEUSLinearArtificialViscosity
Links¶
J. M. Stone and M. L. Norman. “Zeus-2D: A radiation magnetohydrodynamics code for astrophysical flows in two space dimensions. I. The hydrodynamics algorithms and tests.” The Astrophysical Journal Supplement, 80:753, 1992 link
J. M. Stone and M. L. Norman. “Zeus-2D: A radiation magnetohydrodynamics code for astrophysical flows in two space dimensions. II. The magnetohydrodynamic algorithms and tests.” The Astrophysical Journal Supplement, 80:791, 1992 link
Method 3: MUSCL¶
New in version 2.0.
The MUSCL [1] scheme is a second-order accurate extensive of Godunov’s method for solving the hydrodynamics in one dimension. The implementation in Enzo uses second-order Runge-Kutta time integration. In principle, it can use any number of Riemann solvers and interpolation schemes. Here we list the compatible ones that are currently implemented.
Parameters¶
Parameter file call: HydroMethod = 3
RiemannSolver: specifies the type of solver, where the following only works with the MUSCL solver.
- HLL (Harten-Lax-van Leer): a two-wave, three-state solver with no resolution of contact waves.
- LLF (Local Lax-Friedrichs) is based on central differences instead of a Riemann problem. It requires no characteristic information. This is the most diffusive of the available three solvers in MUSCL.
- HLLC (Harten-Lax-van Leer with Contact): a three-wave, four-state solver with better resolution of contacts. The most resilient to rarefaction waves (e.g. blastwave interiors).
If negative energies or densities are computed, the solution is corrected using a more diffusive solver, where the order in decreasing accuracy is HLLC -> HLL -> LLF.
ReconstructionMethod: specifies the type of interpolation scheme used for the left and right states in the Riemann problem.
- PLM: default
- PPM: Currently being developed.
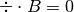 , it uses the hyperbolic cleaning method of
Dedner et al. (2002, JCP 175, 645).
, it uses the hyperbolic cleaning method of
Dedner et al. (2002, JCP 175, 645).