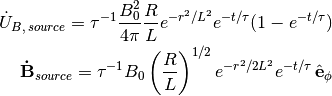Star, Black Hole and Sink Particles¶
There are many different subgrid models of star formation and feedback
in the astrophysical literature, and we have included several of them
in Enzo. There are also methods that include routines for black hole,
sink, and Pop III stellar tracer formation. Here we give the details
of each implementation and the parameters that control them.
For relevant parameters please also see
Star Formation and Feedback Parameters. Note that this section is
particularly detailed because users are generally quite interested
in the differences between the methods. Note also that multiple star
particle creation routines can be used simultaneously with the
StarParticleCreation parameter, as it uses a bitmask - see the
parameter link above for more information.
- Method 0: Cen & Ostriker
- Method 1: Cen & Ostriker with Stochastic Star Formation
- Method 2: Global Schmidt Law
- Method 3: Population III Stars
- Method 4: Sink Particles
- Method 5: Radiative Stellar Clusters
- Method 6: Reserved for future use
- Method 7: Cen & Ostriker with no delay in formation
- Method 8: Springel & Hernquist
- Method 9: Massive Black Holes
- Method 10: Population III stellar tracers
- Method 11: Molecular Hydrogen Regulated Star Formation
- Method 14: Kinetic Feedback
- Restarting a Simulation With Star Formation or Feedback
- Active Particle Framework
- Magnetic Supernova Feedback
Method 0: Cen & Ostriker¶
Select this method by setting StarParticleCreation = 1.
Source: star_maker2.F
This routine uses the algorithm from Cen & Ostriker (1992) that creates star particles when the following six criteria are met
- The gas density is greater than the threshold set in the parameter
StarMakerOverDensityThreshold. This parameter is in code units (i.e. overdensity with respect to the mean matter density) - The divergence is negative
- The dynamical time is less than the cooling time or the temperature
is less than 11,000 K. The minimum dynamical time considered is
given by the parameter
StarMakerMinimumDynamicalTimein units of years. - The cell is Jeans unstable. (Note: this may not be useful depending on your physical resolution! Be very careful with this!)
- The star particle mass is greater than
StarMakerMinimumMass, which is in units of solar masses. - The cell does not have finer refinement underneath it.
These particles add thermal and momentum feedback to the grid cell that contains it until 12 dynamical times after its creation. In each timestep,
![M_{\rm form} &= M_0 [ (1+x_1) \exp(-x_1) - (1+x_2) \exp(-x_2) ]\\
x_1 &= (t - t_0) / t_{\rm dyn}\\
x_2 &= (t + dt - t_0) / t_{\rm dyn}](../_images/math/2e003bc574e1f7969e1b20c648145f4ba83f0710.png)
of stars are formed, where M0 and t0 are the initial star particle mass and creation time, respectively.
- Mej = Mform *
StarMassEjectionFractionof gas are returned to the grid and removed from the particle. - Mej * vparticle of momentum are added to the cell.
- Mform * c2 *
StarEnergyToThermalFeedbackof energy is deposited into the cell. - Mform * ((1 - Zstar) *
StarMetalYield+StarMassEjectionFraction* Zstar) of metals are added to the cell, where Zstar is the star particle metallicity. This formulation accounts for gas recycling back into the stars.
Method 1: Cen & Ostriker with Stochastic Star Formation¶
Select this method by setting StarParticleCreation = 2.
Source: star_maker3.F
This method is suitable for unigrid calculations. It behaves in the same manner as Method 1 except
- No Jeans unstable check (Note: removing this check may be more broadly desirable, depending on your spatial resolution)
- Stochastic star formation: Keeps a global sum of “unfulfilled”
star formation that were not previously formed because the star
particle masses were under
StarMakerMinimumMass. When this running sum exceeds the minimum mass, it forms a star particle. - Initial star particle velocities are zero instead of the gas velocity as in Method 1.
- Support for multiple metal fields.
Method 2: Global Schmidt Law¶
Select this method by setting StarParticleCreation = 4.
Source: star_maker4.F
This method is based on the Kravtsov (2003) paper that forms star particles that result in a global Schmidt law. This generally occurs when the gas consumption time depends on the local dynamical time.
A star particle is created if a cell has an overdensity greater than
StarMakerOverDensityThreshold. The fraction of gas that is
deposited into the star particle is
dt/StarMakerMinimumDynamicalTime up to a maximum of 90% of the gas
mass. Here the dynamical time is in units of years.
Stellar feedback is accomplished in the same way as Method 1 (Cen &
Ostriker) but Mform = StarMakerEjectionFraction * (star
particle mass).
Method 3: Population III Stars¶
Select this method by setting StarParticleCreation = 8.
Source: pop3_maker.F
This method is based on the Abel et al. (2007) paper that forms star particles that represents single metal-free stars. The criteria for star formation are the same as Method 1 (Cen & Ostriker) with the expection of the Jeans unstable check. It makes two additional checks,
- The H2 fraction exceeds the parameter
PopIIIH2CriticalFraction. This is necessary because the cooling and collapse is dependent on molecular hydrogen and local radiative feedback in the Lyman-Werner bands may prevent this collapse. - If the simulation tracks metal species, the gas metallicity in an
absolute fraction must be below
PopIIIMetalCriticalFraction.
Stellar radiative feedback is handled by the Radiative Transfer
module. By default, only hydrogen ionizing radiation is considered.
To include helium ionizing radiation, set PopIIIHeliumIonization
to 1. Supernova feedback through thermal energy injection is done by
the Star Particle Class. The explosion energy is computed from
the stellar mass and is deposited in a sphere with radius
PopIIISupernovaRadius in units of pc. To track metal
enrichment, turn on the parameter PopIIISupernovaUseColour.
Method 4: Sink particles¶
Select this method by setting StarParticleCreation = 16.
Source: sink_maker.C
Multiple variations on this method exist but are not being actively maintained.
They require a completely different set of parameters to turn on such as BigStarFormation;
see Grid_StarParticleHandler.C and Star Formation and Feedback Parameters.
Source: star_maker8.C, star_maker9.C
Method 5: Radiative Stellar Clusters¶
Select this method by setting StarParticleCreation = 32.
Source: cluster_maker.F
This method is based on method 1 (Cen & Ostriker) with the Jeans unstable requirement relaxed. It is described in Wise & Cen (2009). The star particles created with this method use the adaptive ray tracing to model stellar radiative feedback. It considers both cases of Jeans-resolved and Jeans unresolved simulations. The additional criteria are
- The cell must have a minimum temperature of 10,000 K if the
6-species chemistry model (
MultiSpecies == 1) is used and 1,000 K if the 9-species chemistry model is used. - The metallicity must be above a critical metallicity
(
PopIIIMetalCriticalFraction) in absolute fraction.
When the simulation is Jeans resolved, the stellar mass is instantaneously created and returns its luminosity for 20 Myr. In the case when it’s Jeans unresolved, the stellar mass follows the Cen & Ostriker prescription.
Method 6: Reserved for future use¶
This method is reserved for future use.
Method 7: Cen & Ostriker with no delay in formation¶
Select this method by setting StarParticleCreation = 128.
Source: star_maker7.F
This method relaxes the following criteria from the original Cen & Ostriker prescription. See Kim et al. (2011) for more details. It can be used to represent single molecular clouds.
- No Jeans unstable check
- No Stochastic star formation prescription that is implemented in Method 1.
- If there is a massive black hole particle in the same cell, the star particle will not be created.
The StarMakerOverDensity is in units of particles/cm3 and
not in overdensity like the other methods.
Method 8: Springel & Hernquist¶
Select this method by setting StarParticleCreation = 256.
Source: star_maker5.F
This method is based on the Springel & Hernquist method of star formation described in MNRAS, 339, 289, 2003. A star may be formed from a cell of gas if all of the following conditions are met:
- The cell is the most-refined cell at that point in space.
- The density of the cell is above a threshold.
- The cell of gas is in the region of refinement. For unigrid, or AMR-everywhere simulations, this corresponds to the whole volume. But for zoom-in simulations, this prevents star particles from forming in areas that are not being simulated at high resolution.
If a cell has met these conditions, then these quantities are calculated for the cell:
- Cell star formation timescale (Eqn 21 from Springel & Hernquist).
 and
and  are inputs to the model,
and are the star formation time scale and density scaling value,
respectively. Note that
are inputs to the model,
and are the star formation time scale and density scaling value,
respectively. Note that  is not the same as the
critical density for star formation listed above.
is not the same as the
critical density for star formation listed above.  is the
gas density of the cell.
is the
gas density of the cell.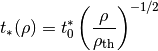
- Mass fraction in cold clouds,
 (see Eqns. 16 and 18).
(see Eqns. 16 and 18). 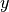 is a dimensionless quantity
calculated as part of the formulation;
is a dimensionless quantity
calculated as part of the formulation;
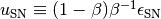 is
the energy released from supernovae back into the gas (note that whether
or not the energy is actually returned to the gas depends on if
is
the energy released from supernovae back into the gas (note that whether
or not the energy is actually returned to the gas depends on if
StarFormationFeedbackis turned on or not);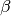 is the
fraction of stars that go supernova soon after formation;
is the
fraction of stars that go supernova soon after formation;
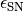 is the energy released from a nominal
supernova and is set to 4e48 ergs; and finally
is the energy released from a nominal
supernova and is set to 4e48 ergs; and finally  is the cooling rate of the cell of gas.
is the cooling rate of the cell of gas.![y\equiv\frac{t_{\ast}\Lambda(\rho,T,z)}{\rho[\beta u_{\mathrm{SN}}-(1-\beta)u_{\mathrm{SN}}]}
x=1+\frac{1}{2y}-\sqrt{\frac{1}{y}+\frac{1}{4y^2}}](../_images/math/4988079d28d8a3bb219bbd2ba6f8c53729068717.png)
- Mass fraction in cold clouds,
Finally, a star particle of mass 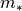 is created with probability
is created with probability
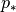 (see
Eqn. 39). For a cell, the quantity
(see
Eqn. 39). For a cell, the quantity 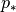 is calculated (below) and
compared to a random number
is calculated (below) and
compared to a random number  drawn evenly from [0, 1).
If
drawn evenly from [0, 1).
If  , a star is created.
, a star is created. 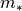 is a parameter of
the model and is the minimum and only star mass allowed;
is a parameter of
the model and is the minimum and only star mass allowed;
 is the mass of gas in the cell;
is the mass of gas in the cell;
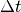 is the size of the simulation time step that
is operative for the cell (which changes over AMR levels, of course).
is the size of the simulation time step that
is operative for the cell (which changes over AMR levels, of course).
![p_{\ast}=\frac{m}{m_{\ast}}\left\{1-\exp\left[-\frac{(1-\beta)x\Delta t}{t_{\ast}}\right]\right\}](../_images/math/046764a96baa8fdceefb2346509bc229c689f15f.png)
If this star formula is used with AMR, some caution is required. Primarily,
the AMR refinement can not be too aggressive. Values of OverDensityThreshold
below 8 are not recommended. This is because if refinement is more aggressive
than 8 (i.e. smaller), the most-refined cells, where star formation should
happen, can have less mass than a root-grid cell, and for a deep AMR hierarchy
the most refined cells can have mass below 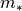 . Put another way,
with aggressive refinement the densest cells where stars should form may be
prevented from forming stars simply because their total mass is too low.
Keeping
. Put another way,
with aggressive refinement the densest cells where stars should form may be
prevented from forming stars simply because their total mass is too low.
Keeping OverDensityThreshold at 8 or above ensures that refined cells have
at least a mass similar to a root-grid cell.
Another reason for concern is in AMR, 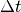 changes with AMR level.
Adding a level of AMR generally halves the value of
changes with AMR level.
Adding a level of AMR generally halves the value of 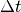 , which
affects the probability of making a star. In a similar way, a small value of
, which
affects the probability of making a star. In a similar way, a small value of
CourantSafetyFactor can also negatively affect the function of this
star formula.
Method 9: Massive Black Holes¶
Select this method by setting StarParticleCreation = 512.
This simply insert a MBH particle based on the information given by an external file (MBHInsertLocationFilename). See Massive Black Hole Particle Formation in Star Formation and Feedback Parameters.
Source: mbh_maker.C
Method 10: Population III stellar tracers¶
Select this method by setting StarParticleCreation = 1024.
Source: pop3_color_maker.F
Method 11: Molecular Hydrogen Regulated Star Formation¶
Select this method by setting StarParticleCreation = 2048.
Source: star_maker_h2reg.F
This SF recipe incorporates ideas from Krumholz & Tan (2007) (KT07), Krumholz, McKee, & Tumlinson (2009) (KMT09) and McKee & Krumholz (2010) (MK10). The star formation rate density is given by:
The SF time scale is the gas free fall time (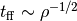 ), and thus the SFR density is effectively proportional to
), and thus the SFR density is effectively proportional to
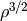 .
.  (
(H2StarMakerEfficiency)
is the specific star formation efficiency per free-fall time, which
typically is around 1% (KT07). The SFR is proportional
to the molecular hydrogen density, not the total gas density. The H2 fraction (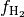 ) is estimated using the
prescription given by KMT09 and MK10, which is based on 1D
radiative transfer calculations and depends on the neutral hydrogen
number density, the metallicity, and the H2 dissociating
flux. The prescription can be written down in four lines:
) is estimated using the
prescription given by KMT09 and MK10, which is based on 1D
radiative transfer calculations and depends on the neutral hydrogen
number density, the metallicity, and the H2 dissociating
flux. The prescription can be written down in four lines:
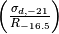 is the ratio of the dust cross section per H nucleus to 1000 Angstroem radiation normalized to 10-21 cm2 (
is the ratio of the dust cross section per H nucleus to 1000 Angstroem radiation normalized to 10-21 cm2 ( ) to the rate coefficient for H2 formation on dust grains normalized to the Milky Way value of 10-16.5 cm3 s-1 (
) to the rate coefficient for H2 formation on dust grains normalized to the Milky Way value of 10-16.5 cm3 s-1 ( ). Both are linearly proportional to the dust-to-gas ratio and hence the ratio is likely independent of metallicity. Although its value is probably close to unity in nature (see discussion in KMT09), Krumholz & Gnedin (2011) argue that in simulations with spatial resolution of ~50 pc, the value of
). Both are linearly proportional to the dust-to-gas ratio and hence the ratio is likely independent of metallicity. Although its value is probably close to unity in nature (see discussion in KMT09), Krumholz & Gnedin (2011) argue that in simulations with spatial resolution of ~50 pc, the value of  should be increased by a factor of ~30 in order to account for the subgrid clumping of the gas. The value of this ratio can be controlled with the parameter
should be increased by a factor of ~30 in order to account for the subgrid clumping of the gas. The value of this ratio can be controlled with the parameter H2StarMakerSigmaOverR.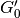 is the H2 dissociating radiation field in units of the typical value in the Milky Way (7.5x10-4 cm3 s-1, Draine 1978). At the moment only a spatially uniform and time-independent radiation field is supported, and its strength is controlled by the parameter
is the H2 dissociating radiation field in units of the typical value in the Milky Way (7.5x10-4 cm3 s-1, Draine 1978). At the moment only a spatially uniform and time-independent radiation field is supported, and its strength is controlled by the parameter H2StarMakerH2DissociationFlux_MW.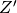 is the gas phase metallicity normalized to the solar neighborhood, which is assumed to be equal to solar metallicity: Z’ = Z/0.02.
is the gas phase metallicity normalized to the solar neighborhood, which is assumed to be equal to solar metallicity: Z’ = Z/0.02.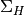 is the column density of the gas on the scale of a giant atomic-molecular cloud complexes, so ~50-100 pc. This column density is calculated on the MaximumRefinementLevel grid cells, and it implies that this star formation method can only safely be used in simulations with sub-100pc resolution. If
is the column density of the gas on the scale of a giant atomic-molecular cloud complexes, so ~50-100 pc. This column density is calculated on the MaximumRefinementLevel grid cells, and it implies that this star formation method can only safely be used in simulations with sub-100pc resolution. If H2StarMakerUseSobolevis set, the column density is calculated through a Sobolev-like approximation,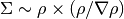 , otherwise it’s simply
, otherwise it’s simply  , which introduces an undesirable explicit resolution dependence.
, which introduces an undesirable explicit resolution dependence.If
H2StarMakerAssumeColdWarmPressureBalance == 1, then the additional assumption of pressure balance between the Cold Neutral Medium (CNM) and the Warm Neutral Medium (WNM) removes the dependence on the H2 dissociating flux (KMT09). In this case![\chi = 2.3 \left( \frac{\sigma_{d,-21}}{R_{-16.5}} \right) \frac{1 + 3.1 \, Z'^{0.365}}{\phi_{\rm CNM}}, \qquad {\rm [KMT09 \; Eq.(7)]}](../_images/math/744ed358b9151791a0c3547995a663b51adf027a.png)
where 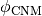 is the ratio of the typical CNM density
to the minimum density at which CNM can exist in pressure balance with
WNM. Currently
is the ratio of the typical CNM density
to the minimum density at which CNM can exist in pressure balance with
WNM. Currently 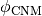 is hard-coded to the value of 3.
is hard-coded to the value of 3.
It is possible to impose an H2 floor in cold gas, which might
be applicable for some low density situations in which the KMT09
equilibrium assumption may not hold. The parameter
H2StarMakerH2FloorInColdGas can be used to enforce such a floor
for all cells that have temperature less than
H2StarMakerColdGasTemperature. This has not been extensively
tested, so caveat emptor.
Optionally, a proper number density threshold
(H2StarMakerNumberDensityThreshold) and/or an H2 fraction
threshold (H2StarMakerMinimumH2FractionForStarFormation) is
applied, below which no star formation occurs.
Typically this method is used with
StarFormationOncePerRootGridTimeStep, in which case SF occurs only
at the beginning of the root grid step and only for grids on
MaximumRefinementLevel, but with a star particle mass that is
proportial to the root grid time step (as opposed to the much smaller
time step of the maximally refined grid). This results in fewer and
more massive star particles, which improves computational
efficiency. Even so, it may be desirable to enforce a lower limit to
the star particle mass in some cases. This can be done with the
parameter H2StarMakerMinimumMass, below which star particles are
not created. However, with H2StarMakerStochastic, if the
stellar mass is less than H2StarMakerMinimumMass, then a star
particle of mass equal to H2StarMakerMinimumMass is formed
stochastically with a probability of (stellar
mass)/H2StarMakerMinimumMass.
Important Note: There is no feedback scheme corresponding to this star maker, so don’t set StarParticleFeedback = 2048. Instead the user should select one of the feedback schemes associated with the other star makers (StarParticleFeedback = 4 comes to mind).
Method 14: Kinetic Feedback¶
Select this method by setting StarParticleCreation = 16384 and
StarParticleFeedback = 16384.
Source: star_maker3mom.F
This method combines stochastic Cen & Ostriker star formation (method 1) with a method for injecting both kinetic and thermal feedback energy into the grid.
The star formation method is identical to method 1, which supplements the star formation perscripton of Cen & Ostriker (1992) with a stochastic star formation recipe. Like method 1, there is no Jeans instability check, however, unlike method 1, the particle velocity is set to the gas velocity.
This star feedback method is described fully in Simpson et al. (2015) (S15). Feedback energy, mass and metals are injected into a 3x3x3 CIC stencil cloud that is centered on the particle position and mapped onto the physical grid. The outer 26 cells of the cloud stencil impart kinetic energy to the physical grid. The amount of momentum injected into each cell is computed assuming a fixed budget of kinetic energy and the direction of the injected momentum is taken to point radially away from the star particle.
CIC stencil overlap with the physical grid. The direction of imparted momentum is indicated with arrows. [Figure 1 S15]
As with methods 0 and 1, the total amount of feedback energy injected into the grid in a given timestep is
- Mform * c2 *
StarEnergyToThermalFeedback
This energy is divided between thermal and kinetic energies. This is despite
the name of StarEnergyToThermalFeedback, which would indicate that it is
just thermal energy. This name was kept for consistency with other star
makers.
If StarMakerExplosionDelayTime is negative, Mform is computed
as it is for star maker methods 0 and 1 as described above. If
StarMakerExplosionDelayTime >= 0.0 then Mform is the initial
star particle mass. In this case, all energy, mass and metals are injected
in a single timestep that is delayed from the formation time of the star
particle creation by the value of StarMakerExplosionDelayTime, which
is assumed to be in units of Myrs. When the feedback is done in a discrete
explosion, the star particle field called dynamical_time is instead used
as a binary flag that indicates wheter the particle has done its feedback
or not (it is set to 1 pre-explosion and 0 once the explosion has been done).
When StarMakerExplosionDelayTime < 0.0, dynamical_time has its
usual meaning.
The amount of energy that takes kinetic form is fixed to be
- Mform * c2 *
StarEnergyToThermalFeedback* fkin
If StarFeedbackKineticFraction is between 0.0 and 1.0, fkin =
StarFeedbackKineticFraction. If StarFeedbackKineticFraction < 0.0,
then fkin is variable and depends on the gas density, metallicity and
resolution surrounding the star particle at the time of the injection.
Equations (16), (17) and (18) in S15 describe how this variable fraction
is computed.
The injection of mass and metals is distributed evenly over the CIC stencil
cloud and is done in proportion to Mform as described in method 0.
The same parameters that control the mass and yield of ejected material are
the same (i.e. StarMassEjectionFraction and StarMetalYield).
The discrete explosion mode and the variable kinetic energy injection mode are intended for use with low mass star particles which produce energy equivalent to only one or a few supernovae.
Restarting a Simulation With Star Formation or Feedback¶
Sometimes it is convenient to run a simulation for a while until it comes to some sort of equilibrium before turning on star formation.
If a simulation is initialized with star formation and feedback turned off, particles in the simulation will not have the necessary particle attribute fields Enzo uses to track data like the formation time, dynamical time, and metallicity.
To restart a simulation including star formation or feedback, simply edit
the parameter file written to disk in the data dump folder (i.e. for a dataset
named DD0100, the parameter file will typically be named DD0100/DD0100.
Change the parameters StarParticleCreation or StarParticleFeedback to
the values needed for your simulation, and restart the simulation. Enzo will
detect that it needs to create particle attribute fields and allocate the
necessary memory above what is needed to read in the dataset.
Distributed Stellar Feedback¶
The following applies to Methods 0 (Cen & Ostriker) and 1 (+ stochastic star formation).
The stellar feedback can be evenly distributed over the neighboring
cells if StarFeedbackDistRadius > 0. The cells are within a cube
with a side StarFeedbackDistRadius+1. This cube can be cropped to
the cells that are StarFeedbackDistCellStep cells away from the
center cell, counted only in steps in Cartesian directions. Below we
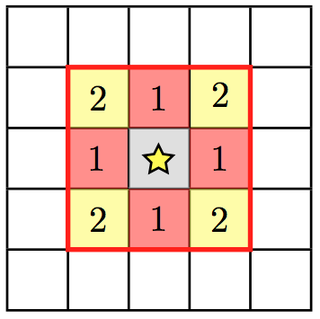
show a couple of two-dimensional examples. The number on the cells indicates the number cell steps each is from the central cell.
StarFeedbackDistRadius = 1
Only cells with a step number <= StarFeedbackDistCellStep have feedback applied to them. So, StarFeedbackDistCellStep = 1 would result in only the cells marked with a “1” receiving energy. In three-dimensions, the eight corner cells in a 3x3x3 cube would be removed by setting StarFeebackDistCellStep = 2.
StarFeedbackDistRadius = 2
Same as the figure above but with a radius of 2.
Feedback regions cannot extend past the host grid boundaries. If the region specified will extend beyond the edge of the grid, it is recentered to lie within the grid’s active dimensions. This conserves the energy injected during feedback but results in the feedback sphere no longer being centered on the star particle it originates from. Due to the finite size of each grid, we do not recommend using a StarFeedbackDistRadius of more than a few cells.
Also see Star Formation and Feedback Parameters.
Notes¶
The routines included in star_maker1.F are obsolete and not
compiled into the executable. For a more stable version of the
algorithm, use Method 1.
Active Particle Framework¶
To be added.
Magnetic Supernova Feedback¶
Source: hydro_rk/SuperNovaSeedField.C
Select this method by setting UseMagneticSupernovaFeedback = 1
(Default = 0) and specifying the parameters below. If
UseMagneticSupernovaFeedback == 2, the parameters
MagneticSupernovaRadius and MagneticSupernovaDuration will
be calculated to be the minimum allowed values (see below)
at runtime based on the cell width and time step of the most-refined grid.
MagneticSupernovaEnergy (in units of ergs) is the total amount
of magnetic energy to be injected by a single supernova event. Defualt = 1e51
ergs.
MagneticSupernovaRadius (in units of parsecs) gives the scale over
which to inject supernova energy. The injection mechanism normalizes the
spatial exponential decay of the injected supernova energy so that all of the
energy is contained within the specified radius. For this reason, the
MagneticSupernovaRadius should be at least 1.5 times the minimum cell width of
the simulation (in pc). Default = 300 pc.
MagneticSupernovaDuration (in units of years) gives the duration of the
supernova magnetic energy injection. The injection mechanism is normalized so
that all of the MagneticSupernovaEnergy is injected over this
time scale. In order to inject the correct amount of energy, MagneticSupernovaDuration should be set to at least 5
times the minimum time step of the simulation. Default = 50,000 years.
The following applies to all star formation methods that produce a PARTICLE_TYPE_STAR object. Methods 0 (Cen & Ostriker) and 1 (+ stochastic star formation) have been tested extensively. The magnetic feedback method is described fully in Butsky et al. (2017).
When a star cluster particle reaches the end of its lifetime, we inject a toroidal loop of magnetic field at its position in hydro_rk/Grid_MHDSourceTerms. The spatial and temporal evolution of the injected magnetic energy and magnetic field is chosen to be:
where t is the time since the ‘death’ of the star cluster particle,
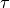 is the
is the SupernovaSeedFieldDuration, R is the cylindrical
radius, r is the spherical radius, and L is the SupernovaSeedFieldRadius.
Two-dimensional schematic overview of the life cycle of a star cluster particle and two channels of its feedback. Left: Star cluster particle formation. Middle: Thermal feedback. Thermal energy by Type II supernova explosion is injected into the gas cell in which a star cluster particle of age less than 120 Myr resides. Right: Magnetic feedback. Toroidal magnetic fields are seeded within three finest cells from a star cluster particle.
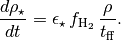
![\chi &= 71 \left( \frac{\sigma_{d,-21}}{R_{-16.5}} \right) \frac{G_0'}{n_H}; \qquad {\rm [MK10 \; Eq.(9)]} \\
\tau_c &= 0.067 \, Z' \, \Sigma_H; \qquad {\rm [KMT09 \; Eq.(22)]} \\
s &= \frac{ \ln( 1 + 0.6 \, \chi + 0.01 \, \chi^2)}{0.6 \tau_c}; \qquad {\rm [MK10 \; Eq.(91)]} \\
f_{\rm H_2} &\simeq 1 - \frac{0.75 \, s}{1 + 0.25 s} \qquad {\rm [MK10 \; Eq.(93)]}](../_images/math/390fb572ce8c0a80444154d821cb4ea63ab8a89c.png)
![CIC stencil overlap with the physical grid. The direction of imparted momentum is indicated with arrows. [Figure 1 S15]](../_images/CIC_momentum.png)