Enzo Particle Masses¶
A common problem for users who wish to manipulate Enzo data is understanding
Enzo’s internal unit system. This is explained in some detail in
Enzo Internal Unit System. This page focuses specifically on the particle mass,
which is one of the least intuitive pieces of the internal code notation. The
most important thing to realize is that Enzo’s particle_mass attribute
*is not a mass* - it is actually a *density*. This is done for a very
good reason - Enzo calculates the gravitational potential by solving Poisson’s
equation using a grid-based density field, and when calculating the dark matter
(or other particle) density, it is most efficient computationally to store it
as a density rather than as a mass to avoid having to divide by volume or
multiple by 1/V for every particle, on every timestep. So, the “mass” stored
within the code is really this value in the cosmology calculations:
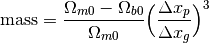
where 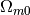 is OmegaMatterNow,
is OmegaMatterNow, 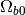 is
OmegaBaryonNow,
is
OmegaBaryonNow, 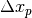 is the mean separation between particles at
the beginning of the simulation (in code units), and
is the mean separation between particles at
the beginning of the simulation (in code units), and 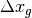 is the
grid spacing (in code units) of the grid that the particle resides in.
Conversion to an actual mass is as follows:
is the
grid spacing (in code units) of the grid that the particle resides in.
Conversion to an actual mass is as follows:
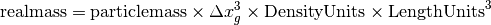
If one is using massive (non-zero mass) particles in a non-cosmology run, the formulation of the particle mass is analogous: it can be calculated as:
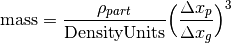
where the upper and lower density values are the mean matter density of your particle field (so total particle mass divided by total volume, in your units of choice) divided by the DensityUnits (such that the fraction is completely unitless).